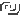Ondřej Klatovský ... dokončení

Andreas Glatoviensis

Třetí traktat o obecném lámání počtu. Při tom algorithmu tolik se species užívá jako při prvním." Praví, že "lámání nic jiného není, toliko díl celé věci, jako 1/3, tj. 1 díl věci na tři rozdělené" a jmenuje "hořejší počet nad linií čtedlník, dolejší jmenovatel." Stejný "čtedlník a jmenovatel činí jednu celou" npř. 2/2, 7/7 atd. "Když jest větší čtedlník nežli jmenovatel, takové lámání víc v sobě nese nežli celá věc" a "když jest menší čtedlník jmenovatele, tehdy takové lámání žádné celé nečiní."
Na to ukazuje jak zlomky počítá, a sice mají-li se dva zlomky rozličných jmenovatelů sečísti, nechť se násobí "křížem" čítatel jednoho jmenovatelem druhého a jmenovatele spolu, taktéž při odčítání; kdyby se však několik zlomků rozličných jmenovatelů mělo sečísti, nechť se sečtou nejprvé dva k součtu nechť se připočte třetí atd.

Dále učí jak se lámání od lámání v obecné lámání, tj. jak se složité zlomky v obyčejné promění, takto: "multiplikůj spolu čtedlníky produkt tvůj obecný čtedlník bude, též podobně multiplikůj jmenovatele produkt tvůj obecný jmenovatel bude," n.p. "2/3 od 3/4 od 1/5 facit 6/60" Pravidla dělitelnosti ještě neznal, neboť praví při zkracování zlomků "kdyby čtedlník i jmenovatel proti pravé ruce měli 0 nebo rovné figury 2, 4, 6, 8, tehdy takový počet skrze 2 dividůj ...; neměli by ti jmenovaní počtové žádného počtu sudou, tehdy najdi počet některý figur lichých jako 3, 5, 7, 9, 11 atd., skrze který bys oba, čtedlník i jmenovatel vyzdvihnouti mohl ..."
Sečítání a odčítání zkouší jako u čísel celých 9ti, a sice dělí čítatele a jmenovatele (dvou sčítanců) 9ti, a napíše zbytky opět v podobě zlomků, pak násobí čítatele, na to násobí jemovatele vespolek, dělí součin opět 9ti a zbytek napíše co jmenovatele nového zlomku; konečně dělí výsledek (součet nebo rozdíl) též 9ti a sice i čítatele i jmenovatele, a zlomek, který tyto zbytky dají, musí se rovnati - je-li dobře počítáno - zbytku předešlému.

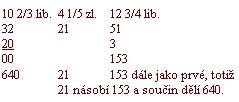
Na to uvádí násobení a dělení zlomků a učí, jak se mají v srovnalosti zlomky odstraniti. Je-li totiž srovnalosť dle předešlého sestavena, násobí se jmenovatel členu třetího jmenovatelem členu druhého a součinem tím čítatel členu prvního, na to pak jmenovatelem členu prvního čítatel členu třetího,
n.p. Jeden koupil 10 lib.2/3 za 4 zl.1/5, zač se dostane 12lib.3/4, facit 5 zl. 5 pen. 19/160; pracuje takto:

Čtvrtý traktat o rozličném běhu kupeckém jest velmi zajímavý a důležitý nejen pro svou stránku praktickou, nýbrž a zvláště pro poznání spůsobu, jakým předkové naši kupčili i s národy zahraničními i doma. Kdo za času Klatovského řešiti chtěl veškeré v traktatu tomto uvedené příklady, musil dokonale znáti pravidla předcházejících tří traktatů a bedlivě pročítati některé zde uvedé návody, což bylo tím nesnadnější, jelikož ona (i tyto) - jak jsme byli viděli - jsou nejen pádná, nýbrž i nepřehledná, zvláště za tou příčinou, že tehdáž nebylo žádných znamének arithmetických.-
Traktát tento jedná o tovaryšství, což jiného nic není, toliko složení peněz dvou neb tří tovaryšův v hromadu; víc a míň, podle každého možnosti, kterýmiž, když zisk vydělají, jak se o něj rozděliti právě mají, a co na každého díl peněz přijíti má, o tom příklady klade "na českou minci."
n.p. Tři se složili v tovaryšství, první dal 20 kop, druhý 33 kop, třetí 45 kop, kterouž sumu vydělali 35 kop, co se dostane z toho na každého?

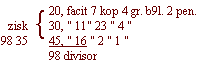
Dělej takto: sumůj v hromadu kopy všech tří, suma bude tvůj divisor, který posaď do regule na první místo proti levé ruce, zisk posaď do prostředku, sumu každého obzvláštně proti pravé ruce na třetí místo, potom děl, přijdeť facit každého takto:

Jiný příklad (důležitý zvláště pro právníka) jest tento:
Jeden měštěnín ležel nemocen k smrti a měl ženu těhotnou, kterýžto udělal kšaft takový:

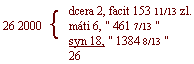
Jest-li by po jeho smrti porodila syna., tehdy ten syn aby 3/4 statku a zboží měl a máti ostatek, jestli by pak dceru porodila, tehdy třetí díl statku aby byl dceři a mateři ostatek. Nu ten jistý měštěnín zemřel, statku po sobě pozůstaviv 2.000 zl. Žena však jeho porodila syna i dceru, otázka co se tomu synu, té dceři a mateři podle kšaftu zřízeného dostati má spravedlivě.
Dělej takto: poněvadž dcera nejméně má, vezmi před sebe počet, který se ti líbí, jako 2, mateři 6, synu 18, ty počty v hromadu sumůj, budeš míti obecný divisor, jako zde:

Na to jedná o měně peněz rozličných zemí, a učí, jak se jedny na druhé převádějí, n.p. kolik rýnských na minci Vídeňskou dá 100 zl. Uherských po 10 šil. a 10 pen.? ("facit 129 rýn. 1 šil. 40 pen."); jak mnoho učiní rýnských zlatých nad sto výše 38 1/9 1234 dukátů? (tj. 100 duk.=138 1/9 rýn. zl., facit 1704 zl. 5 šil. 9 hl. 13/15) atd.

V článku exempla o rozličné koupi a prodaji vysvětluje co jest tara ze sta a návdavek na sto. Po několika příkladech na "dvojitou regula de tri" následují příklady, k jejichž provedení veškerých prv uvedených tvarů početních věděti zapotřebí,
n.p.: Jeden koupil v Norberce 2 sudy kolčův plátna, 1 sud 30 kolčův, dal za jeden kolč 4 zl. bez ortu, stála ho fúra a clo až do Prahy 5 1/2 zl., prodal zase jeden kolč za 4 kopy bez 5ti grošů bíl., 100 kop dá 125 1/5 zl. rýn.; co jest zisku na tom měl? facit 58 zl.rýn. a 3/20 dílů zlatého.
Při regula zisku a ztráty pracuje pomocí srovnalosti,
n.p. Jeden prodal 1 lib. šafránu za 5 zl. 3/4, získal na 100 zl. 10 zl., otázka, co jest ho jedna libra stála, facit 5 zl. 4 šil. 6 hal. 6/11 dílův;
podobně při regula o prostrčení zboží aneb koupi za koupi, kteráž slove od Němcův stich..."
n.p.: Dva chtěli spolu zboží za zboží vyfrejmarčiti, první měl vlnu, druhý sukno, vlny 1 cent. za hotové peníze platil 8 kop, kterýž posadil na prostrčení za 9 kop, balík sukna platil hotových peněz 120 kop.
Otázka jak by měl ten své sukno na prostrčení posaditi, tak aby jeden od druhého sklamán nebyl. Dělej takto a rci 8 kop hotových peněz dá mi na prostrčení 9 kop, co mi dá 120 kop, facit 135 kop, tak draho ten své sukno na prostrčení posaditi má.
Z příkladů, které uvádí na počet stříbra a zlata poznáváme, že hřivna čistého stříbra byla za 8 zl. a hřivna ryzího zlata za 96 zl., poměr stříbra ke zlatu tehdy jako 1:12.

Při regula virginum, od některých jmenuje se coeci uvádí troje řešení každého ze dvou příkladů, jak následuje: 26 osob na jednom kvasu propilo 88 pen. bílých, při tom kvase byli muži, ženy a panny, z mužů 1 osoba dáti měla 6 pen., z žen 4 pen. a z panen jedna 2 pen. Otázka kolik jest při tom cechu anebo kvasu mužů bylo, kolik žen, kolik panen."Pracuje takto: Nejmenším počtem penízů, totiž 2ma násobí počet osob, tj. 26x2=52, které odečte od 88, tak že zbyde 36; pak odečte 2 od 4 a 2 od 6; zbytkem druhým (4mi) dělí 36, aby však ještě něco zbylo pro zbytek první (2) co pro druhého dělitele, vede 4 do 36 pouze 8krát a 2 do zbatku 4 2krát; podíl 8 udává počet mužů a podíl 2 počet žen, zbytek však těchto od 26ti tj. 16 počet panen. Praví dále, že se může 4 do 36 vésti kolikrátkoli n.p. 6 a do zbytku 12 je 2 též 6krát, tak že mohlo býti 6 mužů, 6 žen a 14 panen atd. Je-li určen počet mužů, žen a panen, jest zkouška samozřejmá.

V následujícím článku o lichvě uvádí jeden příklad složitého počtu úrokovému, totiž:
Jeden měštěnín vypůjčil sobě v židech na lichvu 350 kop od jednoho žida, kterýžto na ten spůsob mu půjčil, aby mu každý rok ze 100 kop 5 kop dal, a z těch 105 kop druhý rok aby mu opět lichvu dal tak dlouho, dokud by jich užíval. Ten měštěnín 6 let těch peněz užíval. Otázka, co musí dáti tomu židu z té hlavní sumy zisku a ziskův zisk, tj. lichvu z lichvy.
Pracuje takto:
105 105 105 105 105 105
100 100 100 100 100 100
povýšil 100 a 105 na 6tou mocnosť a sestavil "regula de tri"
1000000000000 . . .1340095640625 . . . 350
z čehož dostal "facit 469 42847/1280000 kop"

Na to uvádí 8 příkladů s návody, jak se má každý řešiti, které jsou ovšem mnohem staršího původu, a s malými změnami v nejnovějších knihách o rovnicích až na nás došly,
n.p. Jeden lovec štval zajíce, kterýž měl napřed výskok 30 skoků, jak často zajíc 6 skoků učinil, tak často chrt za ním 8; otázka, v kolika skocích pes toho zajíce jest uhonil. Dělej takto: odejmi 6 od 8 zůstanou 2; rci 2 skoky budou ukráceny 8, jak mnoho jich umenšeno bude v 30; facit 120, v tolika skocích toho zajíce pes dohoní.

Slušno konečně dotknouti, že v prvním traktatu před charaktera mince a váhy praví : De radice quadrata a cubita nic nepoložím, nebo té species při reguli cosse a alligationis se užívá, časem svým při jmenováných regulích oznámím V knížce této však ani v prvním ani v druhém vydání (úplném) ničehož o cosse a aligaci neuvádí - možná, že napsal jinou arithmetiku, které neznáme.