Ondřej Klatovský ... pokračování

Andreas Glatoviensis

Tomu následuje vyložení charakterů, kterými se váha a mince znamená v těchto knížkách, a po tomto jak se počítá na rozličné mince, z čehož vyjímám jak následuje:
V minci České dělá 30 gr. bílých (a libra) kopu; 24 gr. bílých jest zlatý (rýnský), 1 gr. bílý má 7 penízů bíl.; 1 peníz bílý má 4 haléře, 60 gr. malých jest kopa, 1 groš malý má 7 penízů mal. 1 peníz malý má 2 hal., 6 gr. bíl. jest 1 ort, 4 orty jest 1 zl., 5 ortů jest jedna kopa.
V Norimberské minci jsou 2 hal. 1 peníz, 5 penízů jest 1 paterník, 50 paterníků jest 1 zl., 252 penízů též 1 zl. (patrno, že dva jsou návdavkem), 30 penízů jest 1 pfunt, 8 pfuntův a 12 penízů jest 1 zl. nebo 36 gr.
V Míšenské minci jsou 2 hal. 1 pen., 12. pen. dělá gr., 252 gr. jest 1 zl., 21 gr. též 1 zl. nebo 42 gr. mečových, 60 gr. jest kopa a 20 gr. stará kopa.
V Rakouské a Salcburské minci jsou 2 hal. 1 pen., 30 pen. jest 1 šilink, 8 šilinků dělá 1 zl., 4 pen. jdou do krejcaru a 60 krej. jest též 1 zl.
V Uherské minci jde 100 Uherských penízů na 1 rýnský nebo na 8 šilinků Rakouských, 11 šil. Rak. jest 1 zl. Uherský.
V Bavořích a ve Švábích slove mince černá, a sice jsou 2 hal. 1 peníz, 7 hal. jest krejcar, 30 penízů šilink, 7 šilinků 1 zl., 4 krej. dělají 1 pac nebo rablar a 15 pac též 1 zl.
Šilinky na zlato. 20 šil. jest 1 zl., 5 šil. jest 10 ort a 1 šil. 12 hal.

Dále uvádí rozličné míry a váhy, z nichž pouze vyjímám, že:
32 loket jest postav sukna, 22 postavů jest "saum aneb palík," 22 loket jest 1 barchan, 45 barchanů 1 fordl ... "Na kořenné váze" jest 1061/4 lib. 1 centýř, 6 kamenů v Praze dělá 51/2 kam. v Lipště, 20 kam. v Praze jest 1 centýř atd.
Poněvadž každá věc vysvětlení v příkladech béře, protož pro dokonalé vyrozumění uvádí značný počet příkladů na všechny druhy početní (vyjma dvojnásobení a půlení) s čísly pojmenovanými, bera ohled na veškeré prv uvedené mince, míry a váhy rozličných měst a zemí, tak n.p. u řady arithmetické:
Jeden poslal z Prahy posla do Budína 60 mil. smlouvu takovou učinivše, aby mu od první míle dal jeden peníz malý, od druhé dva, od třetí tři atd. až do 60ti, otázka co mu dá ten jistý za tu cestu?
Přidej první počet k poslednímu učiní 61, půli 60 jest 30, tím multiplikůj 61, učiní 4 kop. miš. 10 grošů bíl. a 5 pen. bíl. -
Častokrát kratochvilné otázky bývají, abys šindely anebo cihly na krově sčetl, což též pomocí řady ukazuje a výkresy znázorňuje.
Na to uváděje regula de tri praví, že se v koupi a prodaji obecné čtyři počtové užívají, tři jsou známi, kteříž v latinském jazyku slovou de tri, protože v sobě tři věci známé nesou, čtvrtá věc neznámá, která z těch tří nalezená bývá. Od kupcův jmenuje se zlatá regule v podobenství, jakožto zlato svou ušlechtilostí jiné všecky kovy převyšuje, tak také tato regule jiné všecky od mathematiků slove regule proportionum... jakž o tom Euklid v svých knihách 5. a 7. naučení dává.
Pravidlo, jak se má jednoduchá "regule de tri" postaviti, udává, jak následuje:

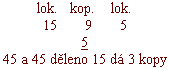
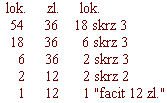
Což věděti chceš, posaď zádu proti pravé ruce, z druhých dvou počtů jeden, kterýž v jmenu a u věci se srovnává s zadním počtem, posaď napřed proti levé ruce ten počet, který jinou věc nese, posaď do prostředku; Multiplikuj prostřední počet spolu s zadním, produkt děl prvním počtem, přijdeť facit v jmenu a u věci rovné prostřednímu počtu;
n.p.: Jeden koupil 15 loket sukna za 9 kop, jak draho přijde 5 loket?

Radí též, aby se, možná-li, zkrátil počet první, a třetí, nebo počet první a druhý, n.p.:

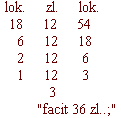
Na to uvádí, že se regula de tri zkouší trojím způsobem, a sice:
1. když se třetí počet na místo prvního a naopak položí, a facit na místo druhé, tedy v uvedeném příkladu:

2. když se "facit" násobí počtem prvním a podobně druhý třetím, součiny musejí si býti rovny,
tj. 12 x 54 = 36 x 18 = 648;
3. když se dané tři členy dělí jakýmkoliv číslem (n.p. 7, 9,11, 13 ...); zbytky se napíší a "facit" se násobí zbytkem prvním, zbytek pak druhý zbytkem třetím, každý součin se opět dělí oním číslem a zbytky musejí si býti rovny, n.p.

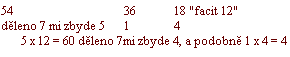
Druhý tractat o počtu na liny.  Při tomto algorithmu se tolik species užívá jako v předešlém, při kterémž jest potřebí znáti numeraci prvního tractatu. Na to vysvětluje, "že první liný," začínaje u spodní, znamená jednu, druhá na ní deset, třetí sto, čtvrtá tisíc, a že každá čtvrtá se znamená křížkem. "Spacium též každé své znamení má, první pod první liný znamená půl, druhé nad první liný pět, třetí mezi druhou a třetí 50"atd. každé znamená 10krát více předešlého. Pak probíraje veškeré druhy početní učí jim na linách jak následuje.

Sečítání vícejmenných čísel n.p.Jeden vybral sumu zlatých a grošů dole sepsanou.

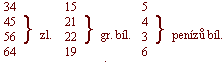
Čísla stejnojmenná se sečtou a součet 199 zl. 77 gr. a 18 penízů se postaví na liny takto:

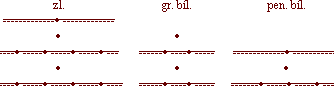
Vzdělej peníze na groše, zdvihni 7 pen. bíl., posaď do pole 1 gr., a to tak často, ažbys neměl co více bráti; groše též také vzdělej na zlaté, vezma 24 gr. za 1 zl. Suma všeho učiní 202 zl. 7 gr. 4 pen.
U odčítání položil se menšenec na liny a menšitel se od něho ubíral (tj. buď se umazával, buď se skutečně grošíky odnímaly), načež zůstal zbytek na linách.
Tomu následuje duplatio a mediatio.
U násobení uvádí Pythagorův stůl čili početní tabulku, načež učí násobiti takto: Když skrze jednu figuru multiplikovati chceš, sáhni na hořejší liny, kde grošíky leží, kteréž multiplikůj s nadepsaným počtem, produkt posaď do druhého pole, ty, kterés multiplikoval, vezmi pryč. A byl-li by na spacium pod prstem 1 grošík, ten neskládaje prstů dolův multiplikůj, též podobně facit do druhého pole vlož. Ten opět multiplikovaný pryč vezmi, s prsem spusť se dolův na druhou liny a dělej jak prvé (produkt do druhého pole klaď) až do konce. Kdyby se n. p. 678 mělo násobiti 2ma, napsal by násobenec liny v levo, jak následuje:

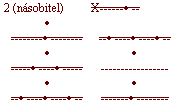
A začínaje s hůry počítalo by se: půl násobeno 2ma dá celou (která by se v pravo na čáru tisíců napsala); 1x2=2 (napíšou se na čáru set dva body), půl násobeno 2ma dá celou (tato se napíše k předešlým dvěma bodům), 2x2=4 a 1/2x2=1, tedy dohromady 5(co se vepíše mezi druhou a třetí čáru), konečně 3x2=6 (napíše se 5 mezi čáru první a druhou a 1 na čáru nejnižsí), součin jest 1356 jak pravé pole ukazuje. Násobení takové jest pravda tím obtížnější, čím více cifer mají činitelé.

Dělení. Počet, který dělen býti má, ten polož na liny, druhý před sebe napiš, skrze který děliti chceš, šetř kolikrát tvůj divisor v počtu nadepsaném vzíti můžeš, tolikrát vezmi a tolik grošíkův do druhého pole polož, kde prstem držíš. Nemohl-li bys celého divisora vzíti, vezmi půl... Při divisi první pole slove druhé a druhé první.
Kdyby se měl předešlý počet 1356 děliti 2ma. položil by se do druhého pole (v pravo) na liny, a pak by se dělilo (začínaje u čáry tisíců): 2 do 1 dá půl (položí se pod čtvrtou čáru do levého pole), 3:2=1 (položí se na čáru třetí) a zbyde 1/2 (která se položí pod předešlou), 5:2=2 (položí se na čáru druhou a 1/2 (pod ní)); konečně 5 a 1 jest 6, 6:2=3 (které se položí na první čáru); podíl se tedy rovná 678. Dělení číslem o dvou a více cifrách jest ovšem mnohem složitější.
Má-li se řada arithmetická na linách sečísti, položí se na první počet s posledním na liny a je-li součet ten sudou, půlí se a touto polovicí násobí; je-li však onen součet lichou, násobí se polovičným počtem členů. Dále učí, jak se na linách vypočítá regula de tri a uvádí pro cvičení-se exempla k obojímu počítání na Českou minci i na váhu atd.
Jelikož příklady tyto nad míru jsou důležité k poznání běhu kupeckého ano i života společenského onoho věku, podávám z nich některé vyňatky vztahující se k ceně rozličného zboží a rozličných výrobků.

Tak se n.p. dovídáme, že centýř vlny byl za 16 kop; kámen vlny za 2 kopy a 10 gr. bíl; libra cínu za 9 gr. míšenských a 5 penízů; libra loje za 4 gr. míš. a 6 pen., kámen sádla za 7 gr. bíl.; loket plátna za 17 pen. malých; "štuka" plátna č. 22 loket za 2 kopy a 20gr.; libra zázvoru za 18 gr. bíl.; libra pepře za 12 gr.; lot hřebíčku za 4 gr. a 2 pen. malé; centýř cukru za 18 zl.; vědro vína "malvazí" za 71/4 zl., "fuder" vína za 14 zl., žejdlík medu za 9 pen. bíl.; vor dříví na vodě (kterých jde 50 na jeden "pramen") za 13 gr. bíl.; pramen dříví za 28 (jinde za 21) kop; strava do roka 35 zl. (rakouské mince); strava za 7 dní 17 krej. (rak. m.); čeledín dostával do roka 15 zl. 19 krej. (rak.m.); 15 vajec za 2 krej. (rak.m.) atp.