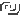Ondřej Klatovský

Andreas Glatoviensis

Odřej narodil se v Klatovech asi r. 1504. Odebrav se později na universitu Pražskou, stal se zde r. 1524 za děkana Tomáše z Vlašimi bakalářem in artibus. O poměrech a stavu muže tohoto nevím nic bližšího, leč že byl znám v domě pana Jana Staršího z Hodějova, známého mecenáše učenců českých,který jej nepochybně podporoval u vydání jeho knihy početní¹⁾.

Ondřej Klatovský zanechal nám nejstarší dosud známou knihu početní, která (jako i pozdější některé spisovatelů jiných) z několika ohledů jest důležitá. Nejprvé z ní poznáváme, jakým spůsobem a jak dalece pěstovala se arithmetika nejen na školách městských veřejně, nýbrž i soukromě v rodinách, z nichž ten neb onen člen se připravoval, aby vstoupil do veřejného, praktického života. Mimo to poučuje nás, jaké mince, míry a váhy času toho se u nás užívalo, a v jakém poměru byly tyto k minci, míře a váze zahraniční, zvláště zemí sousedních, s nimiž předkové naši nejvíce kupčili. Konečně jest však kniha taková za tou příčinou nad míru důležita, jelikož čtouce pilně a bedlivě uvedené v ní příklady, vyňaté ze života praktického, zcela jasně a důkladně si představiti můžeme společenský život praotců svých, a sice nejen jak a s kým kupčili, nýbrž jak živobytí své řídili, vedli, provázeli, ochraňovali a zachovávali. Za těmito příčinami proberu tuto první arithmetiku do podrobna; název její jest:
Nowé knijžky wo počtech na cyfry a liny, přo tom niekteré welmi užitečné regule a exempla mince rozličné, podle biehu kupeckého krátce a užitečnie sebraná skrze práci a náklad Wondřeje Klatowského. V Normberce letha pánie 1530 skrze Frid. Peypusa²⁾

Kniha ta jest v 8erce a má 108 listů, mimo úvod rýmovaný, který začíná³⁾
Šalamoun moudrý vysvědčil, řka, bůh všecky věci stvořil, v  počtu, váze a vzměření, duchovní světské učení a končí tyto knížky když přehlídneš, v krátkém rozumu to najdeš.
Dedikace má nápis: A.G.⁴⁾ poctivému mládenci Svatoslavovi, rodiči Klatovskému, bratru svému pozdravení. V této praví, že na žádost nejmilejšího bratra tuto knížku jemu sepsal řídě se při ní výpovědí Horácovou ... což koli učíš, uč krátce, aby učedlníci rychleji pochopujíce, pamětlivěji toho zachovali.

Jak důležité jsou počty, poznati prý lze z výroků učených mužů, neboť sv. Augustin v svých knihách přikazuje,... aby žádný ani k světskému ani duchovnímu umění nepřistupoval, leč by prvé známosť počtů měl. Plato mudřec přikazuje prý podobně,... aby se mládenci především počtům učili, nebo bez počtů obecní dobré zpravováno býti nemůž; a Pythagoras prý pověděl, ... že ten každý nic neumí, který počítati neumí. Mimo to prý jmenovaný už Plato "rozdíl mezi lidmi a zvířaty klade, že člověk počítati umí," podobně Isiodorus se pronesl, řka, ... odejmi počet od věcí, zhynou všecky, a Šalamoun prý napsal: ... váha a míra spravedlnost jest od pána Boha.

Knížky tyto rozvrhuje Klatovský na čtyři traktaty.
První traktát jedná o počtu na cifry; druhý na liny, při to regula de tri; třetí o lámání počtu a čtvrtý o rozličném běhu kupeckém, k tomu některé regule velmi potřebné.
První traktat má sedm species.
První Numeratio. V této vysvětluje kolik jest "figur" v počtech a jak se vyslovují, klade na každou čtvrtou bod (.), pro cvičení se uvádí několik příkladů. "Všeliký počet v trojím rozdílu se nalézá, kterýž latinskými slovy se jmenuje digitus, articulus a compositus. Digutus slove prst, tj. ten počet, kterýž má znamení svá pod deset... Articulus slove článek, kterýž rovně v deset se dělí 10, 20, 30, 50 ... Compositus slove spolu složený počet z obojího nadepsaného prstu a článku takto 11, 12, 58 ... "
Na to additio - slove sumování, učí mnoho počtův de jedné sumy vnésti." Pro sečítání uvádí trojí zkoušku, a sice odčítání - jsou-li pouze dva sčítanci - pak "druhá proba skrze devět" a třetí "skrze sedm."
O zkoušce devíti praví : Sběř 9 z prvního počtu kolikrát můžeš a to v nic obrať, a co mimi 9 zůstane, to tvá proba. Též podobně z druhého počtu sběř, ostatek tvou probu vzdej s první v hromadu, od kterýž budeš-li moci 9 odvrz, a co mimo to zůstane, státi nech, k tomu s produktu (tak!) sbera, rovna proba se najde. Jestli bys víc počtův před rukama měl, tehdy ze všech sbeř devět, a co mimo 9 zůstane, to tvá proba. Třetí proba skrze sedm jest jistší nežli předešlá skrze devět, kteréž takto užívej. Sbeř 7 s prvního počtu tím obyčejem, jakoby dividovati chtěl, dvě figury spolu bera, a co mimo to zůstane, to tvá proba. Z druhého počtu nejináč též sbeř, ostatek přidej k první probě, od kterých 7 též podobně odvrz, budeš-li moci. Z třetího počtu sumy facit sbera, ostatek rovný má se najiti vrchnímu počtu. Jestli by pak mnoho počtův před rukama měl a je probovati chtěl, tehdy z jednoho každého počtu 7 sbera, proti němu proby státi nech, potom ty proby všech počtův sumůj v hromadu, od kterých též 7 odvrz, zbytku státi nech, potom z sumy též podobně sbeř, proba najde se.
K tomu uvádí tři příklady totiž :

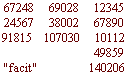
Subtractio slove odjímání anebo odtahování; učí, kterak má se počet od počtu, anebo suma od sumy odjíti, aby poznati mohl co zbytek bude. Při tom praví, že zkoušeti lze, dobře-li počítáno, buď pomocí sečítání, neb devíti, neb sedmi ; n.p.:

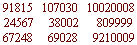
Duplatio a mediatio, ty dvé species zdají se mi zbytečné a daremné zaneprázdnění, nebo duplatio jiného nic není, než skrze 2 multiplacatio, mediatio jest skrze dvě divisio. Protož o nich krátce zavru, při kterýchž není se co zastavovati, neboť multiplicatio a divisio o tom šíř oznamují.⁵⁾Na to zkrátka připomíná, že "duplatio slove dvojení, učí dvakrát větší počet dělati" a že "mediatio slove na poli rozdělování, učí, jak by se měl počet na poli rozděliti" (s příklady).
Multiplicatio slove množení, učí, kterak by měl jeden počet skrze druhý rozmnožiti, k tomu náležité jsou dva počty. Především jest věc potřebná znáti a dobře věděti jednou jedna atd. Na to uvádí čtyry pravidla. První z těchto platí pouze do devíti, a učí v něm, že se mají číslice, které se oběma činitelům nedostávají, do 10 napsati vedle, spolu násobiti a dolení doplněk přes kříž od hořeního činitele odečísti (je-li součin doplňku o jednom čísle, je-li o dvou číslech, musejí se desítky k činiteli přes kříž připočísti)n.p. 9krát 7

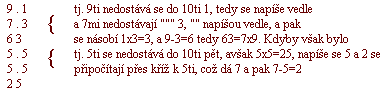
Druhé pravidlo jest podobno prvnímu, platíc též jen o dvou činitelích nejsoucích větší nežli devět. Dle něho má se k menšímu činiteli přidati nicka, od čísla toho má se odečísti činitel druhý (od jedniček pouze) a jedničky, které takto zbudou, mají se násobiti menším činitelem a součet odečísti o 10kráte zvětšeného téhož činitele, n.p.
6 x 5, bude 50 -- méně 6 -- dá 4 násobeno 5ti dá 20 a odečteno od 50ti dá 30 ... Po tomto pravidlu uvádí jednoduchou tabulku početní.
Třetí pravidlo učí, jak se má násobiti číslo nějaké jiným majícím mimo nejvyšší místo samé nicky.
A čtvrté pravidlo poučuje, jak se má násobiti číslem o několika cifrách; před tímto jest provedená velká tabulka početní. Zkoušky příkladů k pravidlu tomuto jsou opět 9ti a 7mi.

Divisio slove dělení, učí větší počet v menší děliti, aby poznati mohl, kolikrát menší počet větším vzat býti můž. Dělení učí takto:

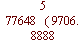
Přisaď dělitele ⁶⁾ pod poslední číslici počtu hořejšího proti levé ruce, aneb byl-li by větší než tato pod předposlední, kolikrát obsažen jest v hoření, napiš v pravo za půlkruh ( a násobiv tím podílem odečti součin od dělence, a pomknuv svým dělitelem o jedno místo dále v pravo děl opět, n.p.:

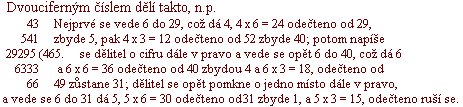
Tříciferným číslem dělí se taktéž, jen že se ovšem stává pracné takové dělení ustavičně složitějším, n.p.

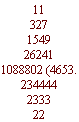
Zkoušky při dělení jsou opět první násobením, druhá devíti sběř 9 kolikrát můžeš jako na předešlých species z divisoru a quotientu, kterýchž zbytky anebo proby multiplikůj, 9 též budeš-li moci odvrz... vezmi také probu z počtu, kterýs dělil, najdeť se rovná proba předešlé; a sedmi, totiž sběř proby z queficientu a z divisoru jako bys divitovati chtěl, prob zbytky spolu multiplikůj, od kterýž též 7, budeš-li moci, odvrz, s počtu, který si dividoval, probu rovnou hořejší najíti máš.

Progressio učí v jednu sumu počty uvésti, kteříž podle přirozeného pořádku anebo jednostejného vypuštění počtu nahoru vcházejí. Dále praví, že "progressio" jest dvojí, totiž přirozená (naturalis, kontinua), která jde prý nahoru žádného počtu nevypouštějíc jako 1, 2, 3, 4, 5, atd. a nepřirozená (discontinua), která rostouc jednostejný počet vypouští, jako 2, 4, 6 atd. Na to učí, jak se určí součet celé řady arithmetické a uvádí něco málo příkladů o řadě měřické, kterou počítá mezi řady nepřirozené a již takto sečítati učí: multiplikůj poslední počet té progresi tím počtem, odkuď se jmenuje (jakož dupla skrze 2, tripla skrze 3 atd.), to udělaje odvrz od produktu první počet té progresi, potom to facit dividůj tím počtem, odkuď ta progrese jméno má méně jedné, produkt ukáže sumu. Zda-liž řada dobře sečtena zkouší jako u sečítání.

1) V 3. dílu "Farrago" str. 234 napsal Matouš Kolínský uvedenému mecenáši, jak následuje: Hoddei, meus Andreas amicus Glatovinus,ab urbe dum pararet discessum,tibi gratias agendas commisit, memorans, sibi quid esset a te difficili suo, gravique nuper tempore praestitum atd.
2) Druhé vydání V Praze r. 1558 u Jana Kantora v Starém Městě Pražském, neliší se hrubě od prvního. Z prvního vydání jest vatištěn úryvek v chrestomatii Tomsově str. 133
3) Až na změněný pravopis doslovně uvádím i dále některá místa, naznačuje tyto znaménkem dokladacím.
4) Andreas Glatoviensis
5) Tato poznámka Klatovského jest důkazem, že sám o věci této přemýšlel, neboť ještě téměř 100 let po nšm uvádějí se "duplatio a mediatio" co zvláštní druhy početní, jako 100 let před ním n.p. mistr Křišťan (v.t.)
6) Klatovský zná pouze jmenovati "divisor" a "quotient," dělenci říká "počet, který se má děliti."