
Jan Burian
honzaburian (at) seznam.cz
You can find here:
Intuitive definitions of complexity
Basics of (complex) systems science
Self-organization and related concepts
Formal definitions of complexity
Very short introduction to modeling methodology
System is an entity in terms of parts and relations between them.
Complex system (complex comes from Latin com- together + plectere to twine or braid) is a system composed from relatively many mutually related parts.
Complex systems are usually (but not always) intricated - hard to describe or understand.
Parts of human society:
- Markets
- Organizations
- Language
- Internet

Biology:
- Cells
- Organ – e.g. brain
- Immune system
- Organisms
- Populations
- Ecosystem
Physics:
- Turbulence
- Weather
- Percolation
- Sandpile

The world consists of many complex systems, ranging from our own bodies to ecosystems to economic systems. Despite their diversity, complex systems have many structural and functional features in common that can be effectively simulated using powerful, user-friendly software. As a result, virtually anyone can explore the nature of complex systems and their dynamical behavior under a range of assumptions and conditions. (M. Ruth, B Hannon, Dynamic Modeling Series Preface)
Structurally complex system
A system that can be analyzed into many components having relatively many relations among them, so that the behavior of each component can depend on the behavior of many others. (Herbert Simon)Remember: The number of relationships could be much higher than the number of components!
Dynamically complex system
A system that involves numerous interacting agents whose aggregate behaviors are to be understood. Such aggregate activity is nonlinear, hence it cannot simply be derived from summation of individual components behavior. (Jerome Singer)
| System types | Simple structure | Complex structure |
| Simple dynamics | Example: Pendulum Model: Analytical - differential equations |
Example: Closed reservoir of gas |
| Complex dynamics |
Example: Double
pendulum |
Example: Ant
pile |
Remember: Interconnection of parts matters in complex systems!

| Reductionism: The properites of the whole system could be explained in terms of its parts. | Holism : The whole system cannot be determined or explained by its component parts alone. Instead, the system as a whole determines in an important way how the parts behave. |
|
|
Pragmatic approach rests on a combination of both reductionism and holism.

The basic rules of the complex systems could be paradoxically very simple, but their effects are intricate and unexpected because of feed-back relations between parts.
Feed-back
The return of a portion of the output of a process or system to the input.
State space (phase space) is an abstract space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the state space. Dimensions of state space represent all relevant parameters of the system. For example state space of mechanical systems has six dimensions and consists of all possible values of position and momentum variables.
Dynamics of the system is the set of functions that encode the movement of the system from one point in the state space to another.
Trajectory of the system is the sequence of system states.
Fixed point is a point in the state space where the system is in equilibrium and does'nt change.
Attractor is a part of the state space where some trajectories end.
Fixed point
Limit cycle
Strange attractor
Dynamical systems can often be modeled by differential equations dx/dt=v(x), where x(t)=(x1(t), …, xn(t)) is a vector of state variables, t is time, and v(x)=(v1(x), …, vn(x)) is a vector of functions that encode the dynamics. For example, in a chemical reaction, the state variables represent concentrations. The differential equations represent the kinetic rate laws, which usually involve nonlinear functions of the concentrations. Such nonlinear equations are typically impossible to solve analytically, but one can gain qualitative insight by imagining an abstract n-dimensional state space with axes x1, …, xn. As the system evolves, x(t) flows through state space, guided by the ‘velocity’ field dx/dt = v(x) like a speck carried along in a steady, viscous fluid. Suppose x(t) eventually comes to rest at some point x*. Then the velocity must be zero there, so we call x* a fixed point. It corresponds to an equilibrium state of the physical system being modeled. If all small disturbances away from x* damp out, x* is called a stable fixed point — it acts as an attractor for states in its vicinity. Another long-term possibility is that x(t) flows towards a closed loop and eventually circulates around it forever. Such a loop is called a limit cycle. It represents a self-sustained oscillation of the physical system. A third possibility is that x(t) might settle onto a strange attractor, a set of states on which it wanders forever, never stopping or repeating. Such erratic, aperiodic motion is considered chaotic if two nearby states flow away from each other exponentially fast. Long-term prediction is impossible in a real chaotic system because of this exponential amplification of small uncertainties or measurement errors. (Strogatz, 2001)
Example: The predator-prey model
We study the dynamics of mutually dependent population size of predators and prey.
The model is supported by analyses of 100 year fur trapping records of the Hudson's Bay Company.

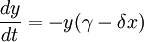
Animation of the system dynamics and the two differential equations governing the dynamics (Lotka-Volterra equations). X represents the size of hare population and Y the size of lynx population.
The portrait of dynamics for different initial x and y parameters forms a fractal.
More information about this fractal.
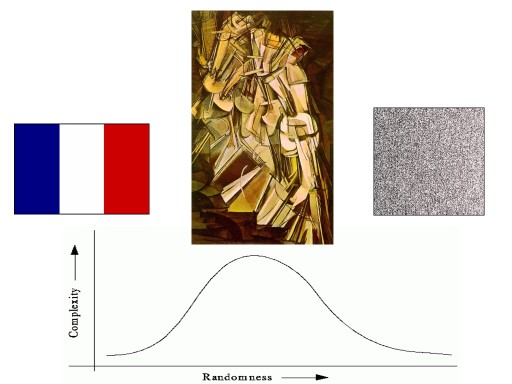
There are many formal definitions of complexity available. Only a small portion of them is suitable for description of complex systems. There are two particular notions of complexity which are not suitable for description of complex systems but have very good sense in other domains.
Good measures of system complexity should measure the amount of regularities in the system (and not its randomness). Such measures should be low for both very simple systems (where is only one or very few dominant regularities) and random systems (where are almost no regularities). Such measures are called non-monotonic. We can say that they are somewhere between order and randomness - on the „edge of chaos“ (Langton, 1990).
Neural complexity (Sporns et al., 2000, 2002) is a measure inspired by the cognitive processes in the brain. It measures how much the change of activity in one part of he network changes the activity in other parts. The authors described it shortly as a measure of "the difference that makes difference". Neural complexity is one of many complexity measures based on mutual information.
Mutual information between two parts of a system is defined:
MI(Xjk,, X-Xjk) = H(Xjk) + H(X- Xjk) – H(X)
There X is the system, Xjk is the j-th permutation of a part of size k and X-Xjk is the rest of the system.
Neural complexity is formally the sum of average mutual information between subsets of the system and the rest of the system
![]()
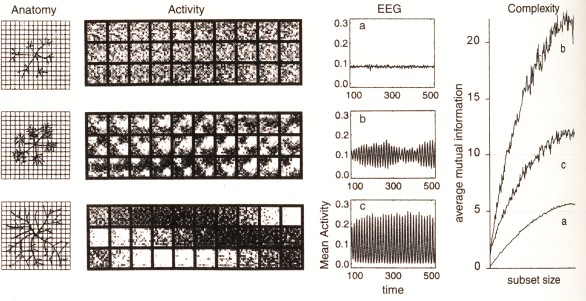
The neural anatomy, neural activity, EEG signal and neural complexity of the brain of an old (a), adult (b) and very young (c) cat. In the old cat there are mostly local specialized connections present but the global integrative connections are missing due to degenrative processes, the result is rather random dynamics. In the adult cat there are both local and global connections present, the result is complex dynamics. In the young cat the local connections are not developed yet but the global connections are already present, the result is regular dynamics (Edelman & Tononi, 2000).
The statistical complexity (Shallizi 2001, 2003, 2004) reflects the intrinsic difficulty of predicting the future states of the system from the system history. It is the amount of information needed about the past of a given point in order to optimally predict its future. Systems with a high degree of local statistical complexity are ones with intricate spatio-temporal organization. Statistical complexity is low both for highly disordered and trivially-ordered systems.
Self-organization (First used by Ashby in 1948.). The ability of the system to autonomously (without being guided or managed by an outside source) increase its complexity.
If a local system is an open system receiving relatively stable and appropriate amount of energy from its environment and the local system is composed from sufficient number of parts which are able to interact through positive and negative feedback, there could (depending on some parameters) be established relatively stable network of feedback loops. This process is called self-organization and the established dynamic network is called self-organized system.
Examples of self-organisation:
In Physics:
Benard cells - coherent motion of large number of molecules in heated liquid layers.
Belousov-Zhabotinsky reactions - a specific "coctail" of chemical ingredients loops through visualy discernable states when it receives thermal (heated) or mechanical (stirred) energy.
In Biology:
Flocking - a group of organism can self-organise in a relatively coherent whole which is able to synchronously react on external stimuli.
Ants demo - increasing the length
of pheromone trace or the number of ants would lead to self-organization
of the food track (result of stigmergic interaction between agents
and environmnent).
An ecosystem or a whole biosphere - the
feedback loops between environment and organism could lead to
stabilisation (homeostatis) of some environmental parameters.
Traditional definition of emergence
The arising of characteristics of the whole which cannot be attributed to the parts. There arise new qualitative and not only quantitative changes. Very vaguely: the whole is more than sum of it parts (an statement made already by Aristotle in Metaphysics).Modern definition
Common characteristics of emergence:
Emergence is „the arising of novel and coherent structures, patterns and properties during the process of self-organization in complex systems." (Corning, 2002; Goldstein, 1999)
- Radical novelty (features not previously observed in the system)
- A global or macro “level” (i.e., there is some property of “wholeness”)
- Coherence or correlation (integrated wholes that maintain themselves over some period of time)
- It is the product of a dynamical process (it evolves)
- It is meaningfull for us (i.e. has some pragmatic value for us – we can use it).
Weak emergence: new properties arising in systems as a result of the interactions at an elemental level. The causal conection between the interactions of the parts and the properties of the whole can be traced in great detail.
In many cases the relationship between parts and the whole depends on large scales of space and time.
| Domain | Elementary level | Global level |
| Geography | Flow of water | Shape of the river bed |
| Brain | Neuronal firing | Synaptical changes |
| Organism | Behaviour in specific situations | Ontogeny |
| Evolution | Life of an individual | Phylogeny |
| Language | Speech acts | Development of language |
| Economy | Activity of micro-economical subjects | Macro-economical properties |
Strong emergence: the properties of the whole supervene on the properties of the parts. Supervenience describes causal dependence between sets of properties. If property B is causaly dependent on property A, it means that one state of property B could be caused by many states of property A, but one state of property A causes exactly one state of property B.
Problems
The combined (cooperative) effects that are produced by two or more particles, elements, parts or organisms – effects that are not otherwise attainable. (Corning, 2002)
Example: Lichen and other symbiotic organisms
Adaptability is the ability of a system to maintain its complexity in changing environment. Often we can find a feed-back between system and its environment.
| System types | Constructed | Self-organized |
| Non-adaptable | Example: Classical machines | Example: Crystals |
| Adaptable | Example: Adaptable robots | Example: Living organisms |

Models:
NetLogo
Daisy world model
Generalized
model at NANIA
History
Characteristics
Basic description of a simple cellular automaton (CA) as presented in
(Wolfram, 2002).
This book is available
on internet and represents a good introduction to cellular
automatons (and other simple automatons with complex behavior) but it
also gained bad reputation due its egocentric tone.
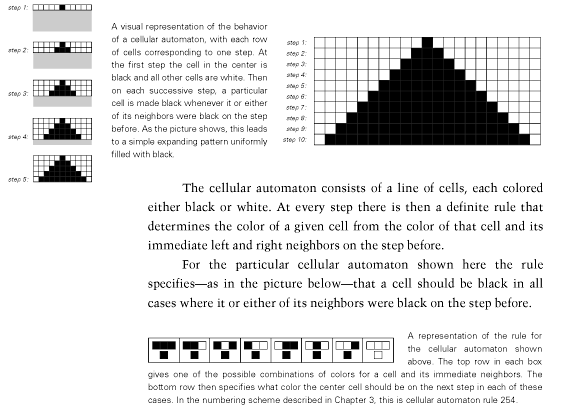
Basic types of rules
Totalistic - the state of the cell is dependent on the sum of neighboring cells with specific states (as in the Game of Life - see the next chapter)
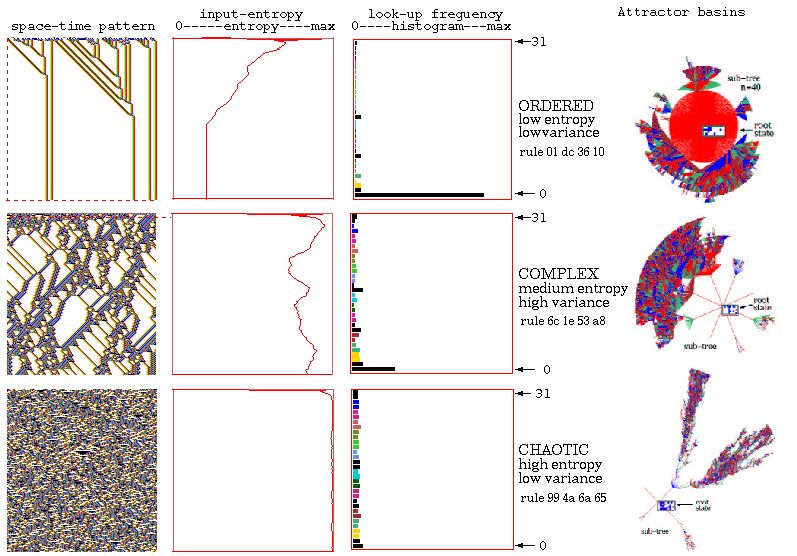
Different rules produce very different behavior.
|
Four classes of behavior in 1D CA (Wolfram,
1983)
|
|||
 |
|||
|
Uniform
|
Repetitive
|
Random
|
Complex
|
|
Types of 2D neighborhood
|
||
 |
||
|
von Neumann
|
Moore
|
Hexagonal
|
Game of Life
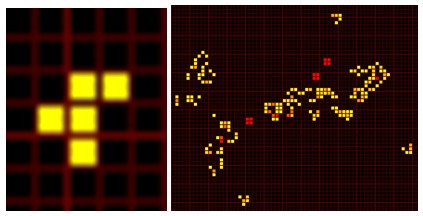
From the five cells on the left (so called F-pentomino) evolved one hundred steps a complex pattern.
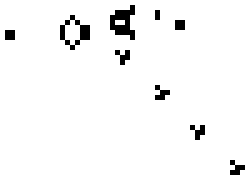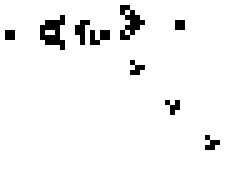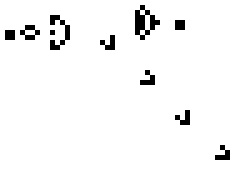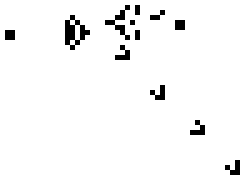

Left: An example of an complex oscilator in Life (Gosper's glider gun). Right: Turing machine implemented in Life (Rendell, 2005).
Self-replication was first investigated by von Neumann in 1940s. The von Neumann self-reproducing automata is actually a universal constructor' that constructs "any machine'' in its 29-state cellular space. In particular, it is capable of Turing universal computation. It solves the self-reproduction problem by reading a tape containing instructions on how to build a copy of itself, provides the copy with a copy of its own input tape, and then presses the ON button starting the copy in operation. In the 1980s, C. Langton and then J. Byl showed that in fact much smaller automata can in fact self-reproduce.
|
Langton's self-replicating loop
|
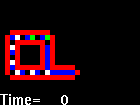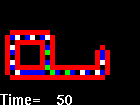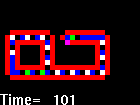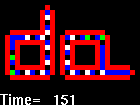 |
|
CA rule 110
|
|
|
A seashell with CA-like patterns
Mireks's Java Cellebration - one of the best CA tools
Game of Life and Cellular automaton on Wikipedia
CA Tutorial by Alexander Schatten,
"History of Cellular Automata" from Stephen Wolfram's "A New Kind of Science"
General article about Cellular Automata by Cosma Shallizi
The DDLab manual by Andy Wuensche with many information about CA, discrete dynamical networks and their attractor basins.
In CA there was interaction possible only between neighbouring cells in a spatial matrix. But the interaction between active parts of a system could be generally described by a network where the active components are represented by nodes and the interactions by edges. Complex networks are a subgroup of networks with "interesting" properties. Natural and social networks are often complex.
Motivation for the study of complex networks:
|
Examples of complex networks
|
|
|
The 1318 transnational corporations that form the core of the economy. (Vitali S. et al., 2011)
Structure of internet (nodes - servers, edges -
connections) |
Biology
|
Structure of yeast protein interactions (nodes - proteins, edges - reactions) (Barabasi et. al., 2003)
Macaque cortex network (Young, 1993) |
For more examples see Gallery of network images
Some properties of complex networks:
|
Types of complex networks (Huang, 2005)
|
||
|
Random network |
Small World network |
Scale-free network |
|
Comparison between the degree distribution of scale-free networks (circle) and random graphs (square) having the same number of nodes and edges. For clarity the same two distributions are plotted both on a linear (left) and logarithmic (right) scale. The bell-shaped degree distribution of random graphs peaks at the average degree and decreases fast for both smaller and larger degrees, indicating that these graphs are statistically homogeneous. By contrast, the degree distribution of the scale-free network follows the power law, which appears as a straight line on a logarithmic plot. The continuously decreasing degree distribution indicates that low-degree nodes have the highest frequencies; however, there is a broad degree range with non-zero abundance of very highly connected nodes (hubs) as well. Note that the nodes in a scale-free network do not fall into two separable classes corresponding to low-degree nodes and hubs, but every degree between these two limits appears with a frequency given by P(k). (Albert, 2005) |
The Potential Implications of Scale-Free Networks (Barabasi et al., 2005):
Chapter about networks in Complex Science for a Complex World.
Exploring complex networks, an article by Strogatz in Nature.
Scale-free networks, an article by Barabasi and Bonabeau in Scientific American.
Models are always “wrong” but sometimes could be useful! (Georg E. P. Box)
A different look at logical relationship between a multiagent
model and reality:
Axelrod (2003) points out: “like deduction model starts with a set
of explicit assumptions. But unlike deduction, it does not prove
theorems. Instead, a simulation generates data that can be analyzed
inductively”. Induction comes at the moment of explaining the behavior
of the model. It should be noted that although induction is used to
obtain knowledge about the behavior of a given model, the use of a model
to obtain knowledge about the behavior of the real world refers to the
logical process of abduction. Abduction, also called inference to the
best explanation, is amethod of reasoning in which one looks for the
hypothesis that would best explain the relevant evidence, as in the case
when the observation that the grass is wet allows one to suppose that it
rained. (Encyclopedia of Complexity)
The term "agent" means an active, autonomous and situated unit.
ABM are a subclass of Multi-agent systems (MAS). Typically in MAS agents could be biological or artificial entitities situated in a real world like a group of animals, group of cooperating robots or virtual entities situated in a non-simulated environment like software agents acting in a computer network. In ABM agents are typically software objects (inter) acting in a simulated environment. ABM could be interpreted as models of real-world MAS.
Which features of real complex systems can we better understand with the help of ABM?
Prisoner's dilemma in game theory
Two agents decide between cooperation and non-cooperation and are
rewarded after their decisions.
Three basic situations could arise:
Iterated prisonner's dilemma (IPD)
The decisions of agents are repeated and rewards accumulated.
The tournament of different playing strategies surprisingly
showed that the best strategy for IPD is very simple:
Tit for Tat: If you cooperate I also cooperate, if you don't cooperate
I also don't cooperate.
If we encode the strategies into a simple genome and evolve competing populations of these strategies the Tit for Tat strategy will evolve spontaneously and become dominant for a reasonable range of rewards.
Other examples:
Applications:
 (Graphic by T. Eymann)
(Graphic by T. Eymann)
Aims of ACE (according to Tesfatsion):
ABM and micro-economical models share the bottom-up approach but in other aspects they substantially differ.
In the process of formalizing a theory into mathematics it is often the case that one or more — usually many! — assumptions are made for purposes of simplification; representative agents are introduced, or a single price vector is assumed to obtain in the entire economy, or preferences are considered fixed, or the payoff structure is exactly symmetrical, or common knowledge is postulated to exist, and so on. It is rarely desirable to introduce such assumptions, since they are not realistic and their effects on the results are unknown a priori, but it is expedient to do so. ... it is typically a relatively easy matter to relax such ‘heroic’ assumptions-of-simplification in agent-based computational models: agents can be made diverse and heterogeneous prices can emerge, payoffs may be noisy and all information can be local.(Axtel, 2000)
|
Micro-economical models
|
ABM
|
|
analytical solutions
|
computational synthesis
|
|
looking for equilibrium
|
dynamical systems often without any equilibrium
|
|
description of behavior
|
emergent behavior
|
|
homogenous agents
|
non-homogenous agents
|
|
based on variables
|
based on relations
|
For comprehensive overview see ACE web pages by Leigh Tesfatsion.
Two particularly interesting models implemented in NetLogo:
Artificial stock market by Carlos Goncalves
Model of market without intermediation by Michal Kvasnička
Advantages
Drawbacks
Examples of extremely simple NetLogo Forrest fire model and its modification for beginners.
Advantages
Drawbacks
For other ABM tools and more detailed comparation see http://en.wikipedia.org/wiki/Comparison_of_agent-based_modeling_software
A guide for newcomers to agent based modeling in the social sciences - by Robert Axelrod and Leigh Tesfatsion
ACE web pages by Leigh Tesfatsion
Agent-based modeling: Methods and techniques for simulating human systems by Eric Bonabeau
Seeing around corners - a popular article about ABM by Jonathan Rauch
Why agents? On the varied motivations for agent computing in the social sciences - an elaborated analysis of relations between ABM and classical analytical models, by Robert Axtell
From factors to actors: Computational sociology and agent-based modeling - sociological approach to ABM by Michael W. Macy and Robert Willer
Complexity of Cooperation Web - by Robert Axelrod
Twenty Years on: The Evolution of Cooperation Revisited - an overview by Robert Hoffmann
Albert, R. J Cell Sci 2005;118:4947-4957
Axelrod, R. (2003): Advancing the Art of Simulation in the Social Sciences. Japanese Journal for Management Information System, Special Issue on Agent-Based Modeling, Vol. 12, No. 3, Dec. 2003.
Axelrod, R. (1987): The Evolution of Strategies in the Iterated Prisoner's Dilemma. In Lawrence Davis (ed.),Genetic Algorithms and Simulated Annealing. London: Pitman, and Los Altos, pp. 32-41. available on WWW: < http://www-personal.umich.edu/~axe/research/Evolving.pdf>.
Barabasi, A. L. Bonabeau, E. Scientific American. New York: May 2003. Vol. 288, Iss. 5; p. 60.
Cools, S.B., C. Gershenson, and B. D'Hooghe (2006): Self-organizing traffic lights: A realistic simulation. available on WWW: < http://uk.arxiv.org/abs/nlin.AO/0610040>.
Corning, Peter A. (2002), The Re-Emergence of "Emergence: A Venerable Concept in Search of a Theory. Complexity 7(6): 18-30
De Wolf, Tom & Tom Holvoet (2005), "Emergence Versus Self-Organisation: Different Concepts but Promising When Combined", Engineering Self Organising Systems: Methodologies and Applications, Lecture Notes in Computer Science: 3464, 1-15. Available on WWW:< http://www.cs.kuleuven.be/~tomdw/publications/pdfs/2005esoa04lncs.pdf >.
Edelman, G. Tononi, G. Universe of consciousness. Basic Book. New York. 2000.
Gell-Mann, M. What Is Complexity?. Complexity. 1995, Vol 1, no.1.
Huang, Chung-Yuan, Sun, Chuen-Tsai and Lin, Hsun-Cheng (2005). Influence of Local Information on Social Simulations in Small-World Network Models. Journal of Artificial Societies and Social Simulation 8(4)8 http://jasss.soc.surrey.ac.uk/8/4/8.html.
J. Goldstein. Emergence as a Construct: History and Issues. Emergence 11: 1999, pp. 49-72.
Hammond, R.A., Axelrod, R. (2005): The Evolution of Ethnocentrism. The Journal of Conflict Resolution. Beverly Hills: Dec 2006. Vol. 50, Iss. 6; pg. 926, 11 pgs.
Hoffmann, R. (2000): Twenty Years on: The Evolution of Cooperation Revisited. Journal of Artificial Societies and Social Simulation vol. 3, no. 2. Available on WWW:< http://jasss.soc.surrey.ac.uk/3/2/forum/1.html>.
Kauffman, S. (1995): At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford University Press.
Langton, C. G. Computation at the edge of chaos. Physica D, 42, 1990.
Lovelock, J.E.; Margulis, L. (1974). "Atmospheric homeostasis by and for the biosphere- The Gaia hypothesis". Tellus 26 (1): 2–10.
Macy, W.M., Willer, R. (2002): From factors to actors: Computational sociology and agent-based modeling. Annual Review of Sociology; 2002; 28, pg. 143
Paul Rendell (2005). [online] . A Turing Machine in Conway's Game of Life. [cit. 1.5.2010]. Dostupné na WWW: < http://rendell-attic.org/gol/tm.htm >.
Salamon, T. Design of Agent-Based Models : Developing Computer Simulations for a Better Understanding of Social Processes. Repin, Czech Republic: Bruckner Publishing. 2011. WWW: <http://www.designofagentbasedmodels.info>
Sporns, O. Tononi, G. and Edelman, G.M. Connectivity and complexity: the relationship between neuroanatomy and brain dynamics. Neural Networks, 13:909–992, 2000. available on WWW <http://php.indiana.edu/~osporns/nn connectivity.pdf>.
Sporns, O. Tononi, G. Classes of network connectivity and dynamics. Complexity, 7:28–38, 2002. available on WWW <http://php.indiana.edu/~osporns/complexity 2002.pdf>.
Shalizi, C. R. and Crutchfield, J. P. Computational mechanics: Pattern and prediction, structure and simplicity. Journal of Statistical Physics, 104:817–879, 2001. available on WWW: <http://arxiv.org/abs/cond-mat/9907176>.
Shalizi, C. R. Optimal nonlinear prediction of random fields on networks. Discrete Mathematics and Theoretical Computer Science, AB(DMCS):11–30, 2003. available on WWW: <http://arxiv.org/abs/math.PR/0305160>.
Shalizi, C. R. Shalizi, L. K. and Haslinger, R. Quantifying self-organization with optimal predictors. Physical Review Letters, 93:118701, 2004. available on WWW: <http://arxiv.org/abs/nlin.AO/0409024>.
Wuensche, A. Discrete Dynamical Networks and their Attractor Basins. In: Complex Systems '98. University of New South Wales, Sydney, Australia. 1998.
Wolfram, S. A New Kind of Science. Wolfram Media. 2002.
Young, L. The organization of neural system in the cerebral cortex. Proceedings of the Royal society. 1993, Series B, 252: 13-18.
Brockman, J. (ed.). Třetí kultura. Academia. Praha. 2008.
Burian, J. Reaktivní multiagentní modely v ekonomii. Doktorská práce. VŠE Praha. 2010. Dostupné na WWW:< http://eldar.cz/cognition/complex/articles/burian_rACE.pdf >.
Burian, J. Multiagentní model transakčních nákladů na finančních trzích. In: Kvasnička, V. Kelemen, J. Pospíchal, J.(eds.). Kognice a umělý život VIII. 2008. Slezská univerzita. Opava. Dostupné na WWW:< http://eldar.cz/honza/articles/burian_ace_fin_market_tc.doc >.
Burian, J. Evoluce averze k riziku a nejistotě. In: Kvasnička, V. Kelemen, J. Pospíchal, J.(eds.). Kognice a umělý život VII. 2007. Slezská univerzita. Opava. Dostupné na WWW:< http://eldar.cz/honza/articles/burian_evoluce_averze.doc >.
Burian, J. Samoorganizace a kognice. In Kelemen, J., Kvasnička V. (eds.). Kognice a umělý život VI. Opava. Slezská univerzita v Opavě. 2005. Dostupné na WWW:< http://eldar.cz/honza/articles/burian_samoorganizae_kognice_final.doc>.
Capra, F. Tkáň života. Academia. Praha. 2004.
Havel, I.M. Přirozené a umělé myšlení jako filosofický problém In: Umělá inteligence III. (V. Mařík a kol., editoři), Academia, Praha 2001, s. 17-75. Dostupné na WWW: < http://www.cts.cuni.cz/reports/1999/CTS-99-11.htm >.
Kauffman, S. Čtvrtý zákon. Paseka. Praha a Litomyšl. 2004.
Kubík, A. Inteligentní agenty. Grada. 2004.
Mandelbrot, B. Fraktály. Mladá fronta. Praha. 2003.
Mařík, V. Štěpánková, O. (Eds.) Umělá inteligence III (kapitola Umělý život). Academia. Praha. 2003.
Pelánek, R. Modelování a simulace komplexních systémů. Nakladatelství Masarykovy univerzity. 2011.
Highfield, R. Coveney, P. Mezi chaosem a řádem. Mladá Fronta. Praha. 2003.